Question

Consider a population list x with μx=10 and SDx = 1. A second population list, y, with μy=10 and SDy=2, is added to the first list. Assuming the same population size for both lists, what is the SD of the new combined list?

Answer 1

The combined standard deviation is 1.58114.

Explanation:

The formula to compute the combined standard deviations of two different data sets is:

`SD_(c) =\sqrt{(n_(X)S^(2)_(X)+n_(2)S^(2)_(Y)+n_(X)(\mu_(X)-\mu_(c))^(2)+n_(Y)(\mu_(Y)-\mu_(c))^(2))/(n_(X)+n_(Y))`

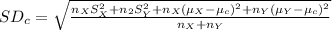
Here
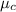`\mu_(c)` is the combined mean given by:

`\mu_(c)=(n_(X)\mu_(X)+n_(Y)\mu_(Y))/(n_(X)+n_(Y))`

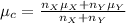
It is provided that the sample size is same for both the data sets, i.e.
`n_(X) = n_(Y)=n`

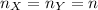
Compute the combined mean as follows:

`\mu_(c)=(n_(X)\mu_(X)+n_(Y)\mu_(Y))/(n_(X)+n_(Y))\\=((n*10)+(n*10))/(n+n)}\\=(20n)/(2n)\\ =10`

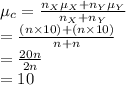
Compute the combined standard deviation as follows:

`SD_(c) =\sqrt{(n_(X)S^(2)_(X)+n_(2)S^(2)_(Y)+n_(X)(\mu_(X)-\mu_(c))^(2)+n_(Y)(\mu_(Y)-\mu_(c))^(2))/(n_(X)+n_(Y))}\\=\sqrt{((n*1^(2))+(n*2^(2))+(n(10-10))+(n(10-10)))/(n+n)}\\=\sqrt{(n+4n)/(2n) } \\=\sqrt{(5n)/(2n) } \\=\sqrt{(5)/(2)} \\=1.58114`

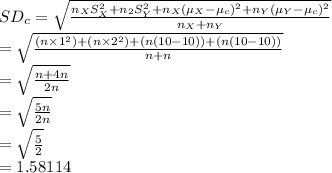
Thus, the combined standard deviation is 1.58114.