Answer:
The combined standard deviation is 1.58114.
Explanation:
The formula to compute the combined standard deviations of two different data sets is:

Here
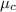 is the combined mean given by:
is the combined mean given by:
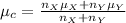
It is provided that the sample size is same for both the data sets, i.e.

Compute the combined mean as follows:
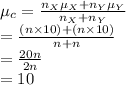
Compute the combined standard deviation as follows:
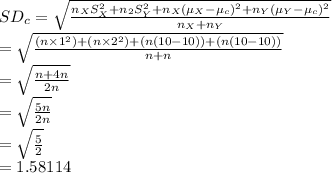
Thus, the combined standard deviation is 1.58114.