Question

pls solve quickly!: It took a boat 2 hours to reach town A going upstream. The way back was 1h20 min. What is the speed of the boat in still water if the speed of the stream is 3 mph?

Answer 1

15 mph

Explanation:

Given: Boat took 2 hours to reach Town A going upstream.

Speed of stream= 3 mph

Time taken to reach back home= 1 hours 20 minutes

Lets assume distance covered one side be "d" and speed of boat in still water be "s".

∴ Speed of boat in upstream=
`(s-3) \ mph`

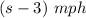
Speed of boat in downstream=
`(s+3)\ mph`

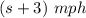
Also converting into fraction of time taken to reach back home.

Remember; 1 hour= 60 minutes

∴ Time taken to reach back home=
`60+20= 80\ minutes`

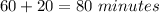
Converting time given into fraction=
`(80\ minutes)/(60\ minutes) = (4)/(3) \ hours`

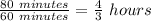
hence, Time taken to reach back home is
`(4)/(3) \ hours`

Now forming equation of boat travelling upstream and downstream, considering distance remain constant.

We know,
`Distance= speed * time`

⇒
`(s-3)* 2= (s+3)* (4)/(3)`

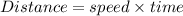
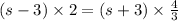
Using distributive property of multiplication

⇒
`2s-6= (4)/(3)s +4`

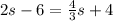
subtracting both side by
`(4)/(3) s`

⇒
`2s-(4)/(3) s-6= 4`

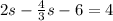
Adding both side by 6

⇒
`2s-(4)/(3) s= 10`

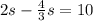
taking LCD as 3

⇒
`(2)/(3) s= 10`

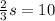
Multiplying both side by
`(3)/(2)`

⇒
`s= (3)/(2) * 10`

∴s= 15 mph

Hence, 15 mph is the speed of the boat in still water.