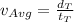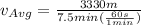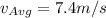Question

In heavy rush-hour traffic you drive in a straight line at 12 m/s for 1.5 minutes, then you have to stop for 3.5 minutes, and finally you drive at 15 m/s for another 2.5 minutes. (a) Plot the position-versus-time graph for this motion. your plot should extend from t=0 to t=7.5 minutes. (b) Use your plot from part (a) to calculate the average velocity between t=0 and t=7.5 minutes.

Answer 1

To develop this problem we will begin to determine the distances traveled in each of the segments using the linear motion kinematic equations. For this purpose, the distance traveled will be determined by the product between speed and time.

Part A is attached and indicates the graph of distance traveled vs time. And the calculations for development are found below. With the distance traveled and the total time it will be possible to find the average speed of the second part.

In 1.5 min the distance covered was,

`d_1 = (1.5 min)((60s)/(1min)) (12m/s) = 1080m`

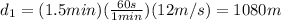
In the next 3.5min the distance covered is 0.

`d_2 = 0`

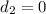
The distance covered for the next 2.5 min is

`d_3 = (2.5 min)((60s)/(1min))(15m/s)=2250m`

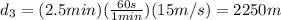
Total distance covered is

`d_T = d_1+d_2+d_3`

`d_T = 1080+0+2250`

`d_T = 3330m`

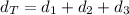
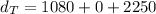
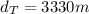
For the average distance we need to use the total distance covered in the total time used. Then,

`v_(Avg) = (d_T)/(t_T)`

`v_(Avg) = (3330m)/(7.5min ((60s)/(1min)))`

`v_(Avg) = 7.4m/s`