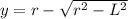Answer:
The particle A will strike on the screen to the right (in -y₀). The particle B will strike to the left of the screen (in y₀), at the same distance than particle A from the x-axis but in the opposite direction. The particle C will strike to the right of the screen (in -y₁), the same direction than particle A, but nearer to the x-axis (see attached image)
The exact positions in the screen are (the point [0,y,0]):
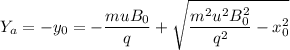
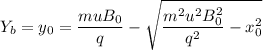
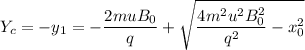
Step-by-step explanation:
The electric charges that move throw a region of space with a magnetic field will suffer a magnetic force (explain by Lorentz Force law). This force will force the particle to change direction but won't change its speed module. Therefore magnetic force act as a centripetal force.
The Lorentz Force law can be written as:

For particle A:
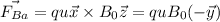
For particle B:
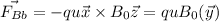
For particle C:
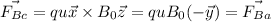
The force applied in each particle in the module is the same as you can see. Nevertheless, their directions are not. In the case of particles A and C, the force has a negative direction in the y-axis while in case B has a positive direction in the y-axis.
Knowing that the magnetic force is a centripetal force, we can find the radius of curvature:
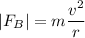
For particle A:
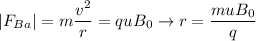
For particle B:
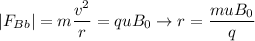
For particle C:
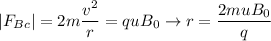
Now we can obtain the exact point in the screen where the particle will strike. We can see than particle A and C are affected by the same force (same module and direction), but the radius of curvature of particle C is twice the one of particle A. Therefore the particle C will strike nearer to the x-axis than particle A.
In each case we can use Pythagoras Theorem to determine the point Y where the particles strike:
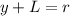 and in the triangle form
and in the triangle form
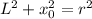
Therefore: