Therefore it is a parallelogram.
Explanation:
Given the vertices of the quadrilateral are A(2,3) , B(7,2), C(6,-1) and D(1,0)
The length of AB is
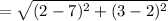
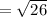 units
units
The length of BC is
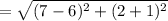
 units
units
The length of CD is

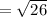 units
units
The length of DA is
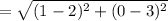
 units
units
The length of AC is
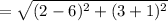
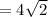 units
units
The length of BD is
 =
=
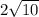 units
units
Here length of AB = length of CD ,
length of BC= length of DA and
length of AC ≠ length of BD
In this quadrilateral, the opposite sides are equal but the diagonals are not equal
Therefore it is a parallelogram.