Final answer:
(a) The resistance of the hose is 8.00 × 10
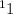 N s
N s
 /m
/m
 .
.
(b) The viscosity of the concrete, assuming laminar flow, is 400 Pa s.
(c) The power being supplied, neglecting the power to increase velocity, is 256 kW.
Explanation:
(a) To determine the resistance of the hose, we can use the Hagen-Poiseuille equation for flow through a cylindrical pipe:
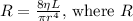 is the resistance,
is the resistance,
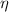 is the viscosity,
is the viscosity,
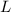 is the length of the hose, and
is the length of the hose, and
 is the radius. Given the length
is the radius. Given the length
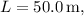 diameter
diameter
 , and pressure
, and pressure
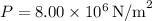 , we find the radius
, we find the radius
 and then calculate the resistance
and then calculate the resistance
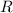 .
.
(b) For laminar flow, the Hagen-Poiseuille equation can be rearranged to solve for viscosity:
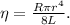 Substituting the known values, including the resistance calculated in part (a), we find the viscosity
Substituting the known values, including the resistance calculated in part (a), we find the viscosity
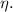
(c) To find the power supplied, we can use the formula
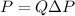 , where \
, where \
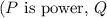 is the flow rate, and
is the flow rate, and
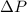 is the pressure difference. Given the flow rate
is the pressure difference. Given the flow rate
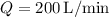 and pressure
and pressure
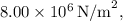 we convert the flow rate to
we convert the flow rate to
 and calculate the power supplied by the pump.
and calculate the power supplied by the pump.