Question

I need the answer to this question.

Answer 1

The value of x is 9.

The value of y is 18.

Explanation:

The given triangle is a right angled triangle.

We have:
`$ tan(x) = (opp)/(adj) $`

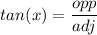
Therefore,
`$ tan(30) = (x)/(9√(3)) $`

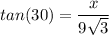
Since,
`$ tan(30) = (1)/(√(3)) $`

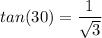
Therefore, we have:

`$ (1)/(√(3)) = (x)/(9√(3)) $`

`$ \implies x = 9 $`

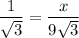
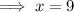
Now, 'y' is the hypotenuse.

Use Pythagoras theorem, we have
`$ x^2 + (9√(3)})^2 = y^2 $`

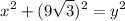
Substituting x = 9, we get:

81 + 81(3) = y²

`$ \implies y^2 = 81 + 243 $`

`$ \implies y^2 = 324 $`

`$ \therefore y = 18 $`

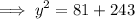
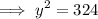
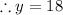
Hence, the value of y = 18.