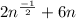Answer: The expression of the marginal cost of producing shoes at n would be :
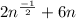
Explanation:
Given : The cost of producing n pair of shoes is given by

Since , the marginal cost of producing shoes at n is the derivative of C at n.
Therefore , Marginal cost function =
![C'(n)=4 ((1)/(2)n^{(1)/(2)}-1)+3(2n)\ \ [\because\ (d\ x^m)/(dx)=mx^(m-1)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/bk7xprxgveza7yz7fqu40ctc3fa3faio2w.png)
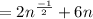
Hence, the expression of the marginal cost of producing shoes at n would be :