Question

n^2-2n-3 where n is the number of key rings in thousands, find the number of key rings sold when the profits is $5,000

Answer 1

For the profit of $5,000, the key chains made is n = 4,000.

Explanation:

Here the given expression , where: n = Number of key rings in thousands is given as:

P(n) = n²- 2 n - 3

Now, Profit is given to be $5,000.

Also, as we know 5000 = 5 x (1,000)

⇒ n²- 2 n - 3 = 5

Now, solving the above expression for the value of n, we get:

`n^2 - 2 n - 3 = 5\\\implies n^2 -2n - 8 = 0\\\implies n^2 -4n + 2n - 8 = 0\\\implies n(n-4) + 2(n-4) = 0\\\implies (n-4) (n+2) = 0`

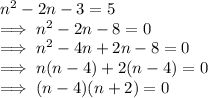
So, n = 4, OR , n = -2

Now, as n = The number of key chains. So it CANNOT BE NEGATIVE.

So, n= 4 = 4 x (1,000) = 4,000 key rings.

Hence, for the profit of $5,000, the key chains made is n = 4,000.