Question

Public surveys were conducted on environmental issues in 2015 and 2016. One of the questions on the survey was: "How serious do you think the atmospheric contamination by exhaust gas is?" In 2015, 420 out of 1090 people surveyed said it was serious, and in 2016, 1063 out of 2,600 people surveyed said it is serious.a) Find a 95% confidence interval for the difference between the two proportions.b) Is there a significant difference at a = 0.05?

Answer 1

95% confidence interval: (-0.0586,0.0106)

Explanation:

We are given the following in the question:

In 2015, 420 out of 1090 people surveyed said it was serious.

`x_1 = 420\\n_1 = 1090\\\\p_1 = \displaystyle(x_1)/(n_1) = (420)/(1090) = 0.385`

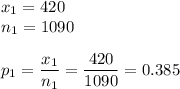
In 2016, 1063 out of 2,600 people surveyed said it is serious.

`x_2 = 1063\\n_2 = 2600\\\\p_2 = \displaystyle(x_2)/(n_2) = (1063)/(2600) = 0.409`

a) Confidence Interval:

`(p_1-p_2) \pm z_(critical)\sqrt{\displaystyle(p_1(1-p_1)/(n_1)+(p_2(1-p_2))/(n_2)}`

`z_(critical)\text{ at}~\alpha_(0.05) = 1.96`

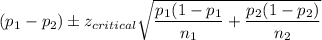
Putting the values, we get:

`(0.385 - 0.409) \pm 1.96\sqrt{\displaystyle(0.385(1-0.385))/(1090)+(0.409(1-0.409))/(2600)}\\\\=-0.024 \pm 0.0346\\=(-0.0586,0.0106)`

b) Since confidence interval contains 0 , hence there is no significant difference at a = 0.05