Question

Picture attached with question

Answer 1

The function is stretched vertically by a factor of 3.

The function shifts 2 to the right.

The function is moved 5 units up.

Step-by-step explanation:

The parent function of the graph is
`f(x)=√(x)`

The transformation for the parent function is given by
`g(x)=3√(x-2) +5`

Thus, the transformed function is in the form of
`y=a√(x-h) +k`

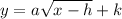
where a is the vertical compression/stretch,

h moves graph to left or right and

k moves the graph up or down.

Thus, from the transformed function
`g(x)=3√(x-2) +5`, we have,

`a=3, h=2 , k=5`

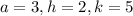
The attached graph below shows the transformation of the graph that the graph is stretched vertically by a factor of 3 and shifted 2 units to the right and moved 5 units up.

Hence, The function is stretched vertically by a factor of 3.

The function shifts 2 to the right.

The function is moved 5 units up.