Question

If the electrical potential energy of two point charges is U when they are a distance d apart, their potential energy when they are fourfold as far apart will be ________.

A. U/4 B. U/2 C. 2U D. 4U

Answer 1

The electric potential energy of the point charges is directly proportional to the charge on the point charged particle and inversely proportional to the distance between the point charges.

Mathematically the general expression is

`U_p = (kq_p)/(r_p)`

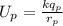
Here,

k = Coulomb's constant

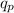`q_p` = Charge

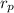`r_p` = Distance

From the aforementioned consideration we have to

`U_p \propto (1)/(r_p)`

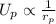
Between two loading states (final and initial) the expression would become

`(U_p)_1 (r_p)_1 = (U_p)_2 (r_p)_2`

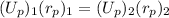
If the distance between the two points is the double
`(r_p)_1 = 2(r_p)_2` we can now write the expression as

`(U_p)_1 r_p = (U_p)_2 (2r_p)`

`(U_p)_2 = ((U_p)_1)/(2)`

Therefore te potential energy when the distance between the point charge is double, is U/2.

Therefore the correct answer is B.