Answer:
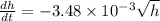 feet per second is the differential equation
feet per second is the differential equation
Step-by-step explanation:
Given:
The radius of the cylindrical tank= 2 feet
The height of the cylindrical tank = 10 feet
The radius of the circular hole = 3/4 inches
To Find:
The differential equation for the height h of the water at time t.
Solution:
Finding the surface area(A) of the tank
Surface area =
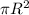
On substituting the values
Surface area =
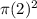
=
 square feet
square feet
Finding the surface area(a) of the hole
The radius is given in inches, so converting into feet we have
1 inch = 0.083 foot
similarly
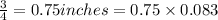 = 0.0625 feet.
= 0.0625 feet.
Now the surface area,
=
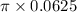
=
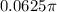 square feet
square feet
Now let the velocity of water through the hole is v
According law of conservation of energy, the penitential energy due to the height h of the water gets converted into kinetic energy.
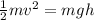
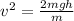
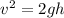
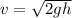
The rate of water flowing through the hole is =
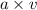
= >

At any time t
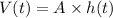
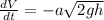
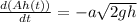
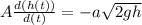
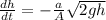
On substituting the values, we get
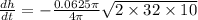
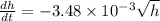 feet per second
feet per second