Question

On a straight road (taken to be in the +x direction) you drive for an hour at 50 km per hour, then quickly speed up to 90 km per hour and drive for an additional two hours.

(a) How far do you go (?x)?
total distance = (...)km
(b) What is your average x component of velocity (vavg,x)
vavg,x = (...)km/hr
(c) Why isn't vavg,x equal to the arithmetic average of your initial and final values of vx, (50+90)/2 = 70 km per hour?

Answer 1

a) 230 Km b) 76.7 km/h c) Please see below

Step-by-step explanation:

a) If we can neglect the time while the driver accelerated, the movement can be divided in two parts, each of them at a constant speed:

`x = x1 + x2 \\\\x1 = 50 km/h* 1hr = 50 km, \\x2 = 90 Km/h*2hr = 180 km\\`

⇒
`x = 50 km + 180 km = 230 km`

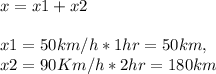
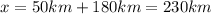
b) The average x component of velocity, can be calculated applying the definition of average velocity, as follows:

`vavg,x = (xf-xo)/(t-to)`

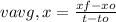
If we choose t₀ = 0 and x₀ = 0, replacing xf and t by the values we have already found, we can find vavg,x as follows:

`vavg,x =(230 km)/(3 hr) =76.7 km/h`

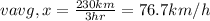
c) The found value of avg,x is not the same as the arithmetic average of the initial and final values of vx (70 Km/h) due to the time traveled at both velocities was not the same.

If the driver had droven half of the time (1.5 h) at 50 km/h and the other half at 90 km/h, total displacement would have been as follows:

`x = 50 km/h*1.5 h + 90 km/h*1.5 hr = 210 km`

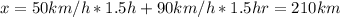
Applying the definition of average velocity once more:

`vavg,x =(210 km)/(3 hr) =70 km/h`

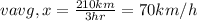
which is the same as the arithmetic average of the initial and final values of vₓ.