Question

An animal-rescue plane flying due east at 55 m/s drops a bale of hay from an altitude of 69 m . The acceleration due to gravity is 9.81 m/s 2 . If the bale of hay weighs 192 N , what is the momentum of the bale the moment it strikes the ground?

Answer 1

The momentum of the bale the moment it strikes the ground is 1076.68 kg-m/s.

Step-by-step explanation:

It is given that,

Velocity of an animal-rescue plane,
`v_x=55\ m/s`

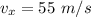
It drops a bale of hay from an altitude of 69 m, h = 69 m

The vertical velocity of plane is given by :

`v_y=√(2gh)`

`v_y=√(2* 9.81* 69) =36.79\ m/s`

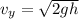
Weight of the bale of hay, W = 192 N

If m is the mass, then weight is given by :

`m=(W)/(g)`

`m=(192)/(9.81)=19.57\ kg`

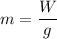
The resultant momentum of the bale the moment it strikes the ground is given by :

`p=m(v_x-v_y)`

`p=19.57* 55i-19.57* 36.79j`

`p=(1076.35i-719.98j)\ kg-m/s`

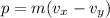
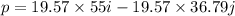
Magnitude of momentum,

`p=\sqrt{1076.35^(2)+719.98}`

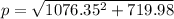
p = 1076.68 kg-m/s

So, the momentum of the bale the moment it strikes the ground is 1076.68 kg-m/s. Hence, this is the required solution.