If P(A) = 0.3, P(B) = 0.2, and P(A and B) = 0.1, determine the following probabilities: (a) P (A') (b) P (A U B) (c) P [(A U B)'] (d) P (A' U B)'

Question

asked Jun 26, 2021 37.6k views

1 Answer

CharlesAE · Answer 1 · 2021-07-02T01:35:16+0000

Answer:

a)
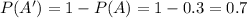
P(A') = 1-P(A) = 1-0.3=0.7

b)
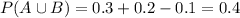
$P(A \cup B) =0.3 +0.2- 0.1=0.4$

c)
$P[(A \cup B)'] = 1-P(A \cup B) = 1-0.4 =0.6$

d) For this case we can find first this probability:

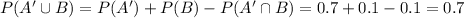
$P(A' \cup B) = P(A') +P(B) -P(A' \cap B) = 0.7+0.1 -0.1 =0.7$

And then using the complement rule we got:

$P[(A' \cup B)']= 1-P(A' \cup B) = 1-0.7=0.3$

Explanation:

For this case we define two events A and B with the following probabilities:

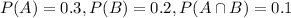
$P(A) =0.3 , P(B) =0.2, P(A \cap B) =0.1$

And we want to find the following probabilities:

(a) P (A')

For this case we can use the complement rule and we got:

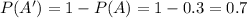
P(A') = 1-P(A) = 1-0.3=0.7

(b) P (A U B)

For this case we can use the total probability rule and we got:

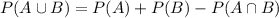
$P(A \cup B) = P(A) +P(B) -P(A \cap B)$

And if we replace we got:

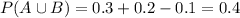
$P(A \cup B) =0.3 +0.2- 0.1=0.4$

(c) P [(A U B)']

For this case we can use the complement rule again and we have this:

$P[(A \cup B)'] = 1-P(A \cup B) = 1-0.4 =0.6$

(d) P (A' U B)'

For this case we can find first this probability:

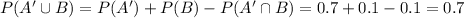
$P(A' \cup B) = P(A') +P(B) -P(A' \cap B) = 0.7+0.1 -0.1 =0.7$

And then using the complement rule we got:

$P[(A' \cup B)']= 1-P(A' \cup B) = 1-0.7=0.3$