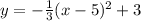Answer:
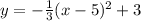
Explanation:
We are given the following;
- Vertex of a quadratic function = (5,3)
- A point where the function passes through (-1, -9)
Required to determine the equation of the function;
- We need to know the vertex form of a quadratic function is;
 , where h and k correspond to the vertex (h,k)
, where h and k correspond to the vertex (h,k)
- Therefore, we can replace the variables h and k of the vertex in the equation;
That is;

Then we use the equation and the point given to solve for a
x = -1 and y = -9
We get;
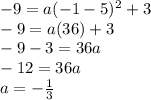
Substituting the values of a, h and k in the equation, we get;
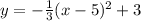
Thus, the equation of the function in the vertex form is