Question

An instructor in a college class recently gave an exam that was worth a total of 100 points. The instructor inadvertently made the exam harder than he had intended. The scores were very symmetric, but the average score for his students was 54 and the standard deviation of the scores was 4 points. The instructor is considering 2 different strategies for rescaling the exam results:Method 1: Add 20 points to everyone's score.Method 2: Multiply everyone's score by 1.5.Which of the following are true?Select all that apply.Select one or more:a. Method 1 will increase the standard deviation of the students' scoresb. Method 2 will increase the standard deviation of the students' scores.c. Method 1 will decrease the standard deviation of the students' scores.d. Method 2 will decrease the standard deviation of the students' scores.

Answer 1

b. Method 2 will increase the standard deviation of the students' scores.

Explanation:

Given that an instructor in a college class recently gave an exam that was worth a total of 100 points.

The average score for his students was 43 and the standard deviation of the scores was 5 points.

And now he is considering two different strategies for rescaling the exam results of which:

• Method 1 = Add 20 points to everyone's score.

• Method 2 = Multiply everyone's score by 1.5 .

And we have to check what will be the impact of these methods on the standard deviation of the students' scores.

For this let us consider a simple example to understand this:

Firstly, Formula for calculating Standard Deviation =
`\sqrt{(\sum (X - Xbar)^(2))/(n-1)}`

Suppose,

X X - Xbar
`(X - Xbar)^(2)`

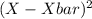
3 3 - 6 = -3 -3 * -3 = 9

5 5 - 6 = -1 -1 * -1 = 1

10 10 - 6 = 4 4 * 4 = 16

Mean of above data, Xbar =
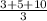`(3+5+10)/(3)` = 6

Standard Deviation of data =
`\sqrt{(26)/(3-1) }` = 3.6055

Now let us suppose that we multiply each value of above data with 2 so the new data will be:

X X - Xbar
`(X - Xbar)^(2)`

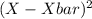
3*2 = 6 6 - 12 = -6 -6 * -6 = 36

5*2 = 10 10 - 12 = -2 -2 * -2 = 4

10*2 =20 20 - 12 = 8 8 * 8 = 64

Mean of new data, Xbar =
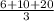`(6+10+20)/(3)` = 12

Standard Deviation of new data =
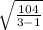`\sqrt{(104)/(3-1) }` = 7.2111

Hence, we see that when we multiply any value to the data the standard deviation will increase and in other words it will multiplied by that value which value we multiplied with each data value i.e. when we multiply each data value with 2 the standard deviation also get multiplied by 2 as 3.6055 * 2 = 7.2111.

Hence, in our question Standard deviation will be 4*1.5 = 6 points when Method 2 is used.

Therefore option B is correct that Method 2 will increase the standard deviation of the students' scores.

And on the other hand Similarly by adding any constant to the data the Standard Deviation will remain same. Therefore Method 1 will have no impact on standard deviation of the students' scores.