Question

2. An observer on top of a 50 foot tall lighthouse sees a boat at a 7 angle of depression. To the nearest foot how far is the boat from the base of the lighthouse ? A. 6 feet B. 50 feet C. 407 feet D. 410 feet

Answer 1

The distance between the boat and the base of the lighthouse is:

C. 407 feet

Explanation:

Given:

Height of lighthouse = 50 ft

Angle of depression from observer to boat = 7°

To find the distance of the boat from the base of the lighthouse.

Solution:

The situation can be represented by a right triangle ABC such that:

m∠ACB =
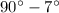`90\°-7\°`= 83°

BC= 50 ft

We need to find length of AB.

Applying trigonometric ratios.

`\tan\theta=(AB)/(BC)`

Plugging in given values.

`\tan83\°=(AB)/(50)`

`8.14=(AB)/(50)`

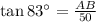
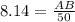
Multiplying both sides by 50

`50* 8.14=(AB)/(50)* 50`

`407=AB`

∴
`AB=407\ ft`

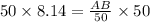
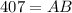
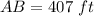
Thus, distance between the boat and the base of the lighthouse 407 feet