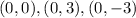Question

Given the relation x = y 4 − 9 y 2, identify the x- and y- axis intercepts.

Answer 1

The x-intercepts are
`(0,0)`

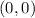
The y-intercepts are
`(0,0),(0,3),(0,-3)`

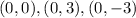
Step-by-step explanation:

The relation is
`x=y^(4) -9y^(2)`

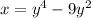
To find the x-intercept, let us substitute
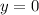`y=0` in the equation
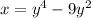`x=y^(4) -9y^(2)`, we get,

`x=(0)^(4) -9(0)^(2) \\x=0`

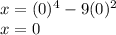
Thus, the x-intercepts are
`(0,0)`

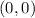
To find the y-intercept, let us substitute
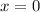`x=0` in the equation
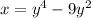`x=y^(4) -9y^(2)`, we get,

`0=y^(4)-9 y^(2)`

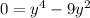
let us switch sides and solving, we get,

`\begin{aligned}y^(4)-9 y^(2) &=0 \\y^(2)\left(y^(2)-9\right) &=0 \\y^(2) &=0, y^(2)-9=0\end{aligned}`

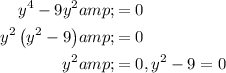
Taking square root,

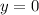`y=0` and
`\begin{aligned}y^(2)-9 &=0 \\y^(2) &=9 \\y &=\pm 3\end{aligned}`

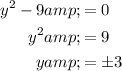
Thus, the y-intercepts are
`(0,0),(0,3),(0,-3)`