Question

If line GH is perpendicular to line HJ, then GJ is ____ HJ.

Choose the relationship symbol that would make a true statement.

A. <

B. =

C. >

Answer 1

Option A: >

Solution:

Given a triangle GHJ.

The line GH is perpendicular to line HJ.

This means the triangle is a right angled triangle.

In ΔGHJ, GH is the base of the triangle and

HJ is a height of the triangle.

Then the third side must be the hypotenuse of the right triangle.

We know that by the Pythagoras theorem,

`(\text {Hypotenuse})^2=(\text{Base})^2+(\text{Height})^2`

`(\text {GJ})^2=(\text {GH})^2+(\text {HJ})^2`

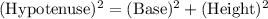
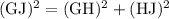
This clearly shows that the hypotenuse is greater than the height.

⇒ GJ > HJ

Option A: > is the correct answer.

If line GH is perpendicular to line HJ, then GJ is > HJ.