Question

.. Which of the following are the coordinates of the vertices of the following square with sides of length a?

A. 0(0,0), S(0,a), 7(a,a),W(a,0)
B. 0(0,0), S(0,a),T (2a, 2a),W (a,0)
C. 0(0,0), (0,2a), 7(2a, 2a),W (20,0)
D. 0(0,0), 5(a,0), 7(a, a),(0,a)

Answer 1

Option A:
`O(0,0), S(0,a), T(a,a), W(a,0)`

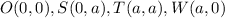
Option D:
`O(0,0), S(a,0), T(a,a), W(0,a)`

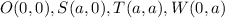
Explanation:

Option A:
`O(0,0), S(0,a), T(a,a), W(a,0)`

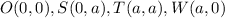
To find the sides of a square, let us use the distance formula,

`d=\sqrt{\left(x_(2)-x_(1)\right)^(2)+\left(y_(2)-y_(1)\right)^(2)}`

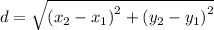
Now, we shall find the length of the square,

`\begin{array}{l}{\text { Length } O S=\sqrt{(0-0)^(2)+(a-0)^(2)}=\sqrt{a^(2)}=a} \\{\text { Length } S T=\sqrt{(a-0)^(2)+(a-a)^(2)}=\sqrt{a^(2)}=a} \\{\text { Length } T W=\sqrt{(a-a)^(2)+(0-a)^(2)}=\sqrt{a^(2)}=a} \\{\text { Length } O W=\sqrt{(a-0)^(2)+(0-0)^(2)}=\sqrt{a^(2)}=a}\end{array}`

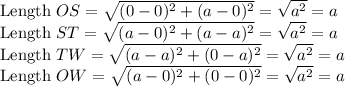
Thus, the square with vertices
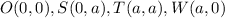`O(0,0), S(0,a), T(a,a), W(a,0)` has sides of length a.

Option B:
`O(0,0), S(0,a), T(2a,2a), W(a,0)`

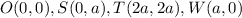
Now, we shall find the length of the square,

`\begin{aligned}&\text { Length } O S=\sqrt{(0-0)^(2)+(a-0)^(2)}=\sqrt{a^(2)}=a\\&\text {Length } S T=\sqrt{(2 a-0)^(2)+(2 a-a)^(2)}=\sqrt{5 a^(2)}=a √(5)\\&\text {Length } T W=\sqrt{(a-2 a)^(2)+(0-2 a)^(2)}=\sqrt{2 a^(2)}=a √(2)\\&\text {Length } O W=\sqrt{(a-0)^(2)+(0-0)^(2)}=\sqrt{a^(2)}=a\end{aligned}`

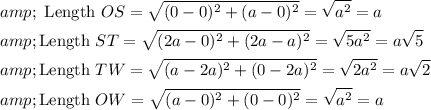
This is not a square because the lengths are not equal.

Option C:
`O(0,0), S(0,2a), T(2a,2a), W(2a,0)`

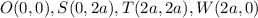
Now, we shall find the length of the square,

`\begin{array}{l}{\text { Length OS }=\sqrt{(0-0)^(2)+(2 a-0)^(2)}=\sqrt{4 a^(2)}=2 a} \\{\text { Length } S T=\sqrt{(2 a-0)^(2)+(2 a-2 a)^(2)}=\sqrt{4 a^(2)}=2 a} \\{\text { Length } T W=\sqrt{(2 a-2 a)^(2)+(0-2 a)^(2)}=\sqrt{4 a^(2)}=2 a} \\{\text { Length } O W=\sqrt{(2 a-0)^(2)+(0-0)^(2)}=\sqrt{4 a^(2)}=2 a}\end{array}`

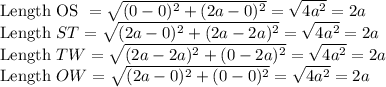
Thus, the square with vertices
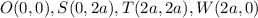`O(0,0), S(0,2a), T(2a,2a), W(2a,0)` has sides of length 2a.

Option D:
`O(0,0), S(a,0), T(a,a), W(0,a)`

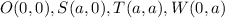
Now, we shall find the length of the square,

`\begin{aligned}&\text { Length OS }=\sqrt{(a-0)^(2)+(0-0)^(2)}=\sqrt{a^(2)}=a\\&\text { Length } S T=\sqrt{(a-a)^(2)+(a-0)^(2)}=\sqrt{a^(2)}=a\\&\text { Length } T W=\sqrt{(0-a)^(2)+(a-a)^(2)}=\sqrt{a^(2)}=a\\&\text { Length } O W=\sqrt{(0-0)^(2)+(a-0)^(2)}=\sqrt{a^(2)}=a\end{aligned}`

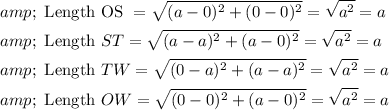
Thus, the square with vertices
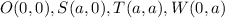`O(0,0), S(a,0), T(a,a), W(0,a)` has sides of length a.

Thus, the correct answers are option a and option d.