Question

Which statement describes the behavior of the function f (x) = StartFraction 2 x Over 1 minus x squared EndFraction?

A. The graph approaches –2 as x approaches infinity.
B. The graph approaches 0 as x approaches infinity.
C. The graph approaches 1 as x approaches infinity.
D. The graph approaches 2 as x approaches infinity.

Answer 1

It's B on edge

Explanation:

Answer 2

Option B.

Explanation:

The given function is

`f(x)=(2x)/(1-x^2)`

We have find the behavior of the function f (x) as x approaches infinity.

The given function can be rewritten as

`f(x)=(2x)/(x^2((1)/(x^2)-1))`

`f(x)=(2)/(x((1)/(x^2)-1))`

`lim_(x\rightarrow \infty)f(x)=lim_(x\rightarrow \infty)(2)/(x((1)/(x^2)-1))`

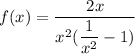
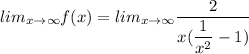
Apply limit.

`lim_(x\rightarrow \infty)f(x)=(2)/(\infty((1)/(\infty^2)-1))`

`lim_(x\rightarrow \infty)f(x)=0`

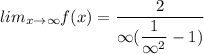
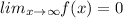
The graph approaches 0 as x approaches infinity.

Therefore, he correct option is B.