Answer:
The values of x and y to the given equations are x=-1 and
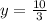
The solution is (-1,
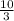 )
)
Explanation:
Given equations are

and

to solve the given equations by elimination method :
Adding the given two equations (1) and (2) we get
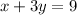
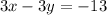
_______________
4x=-4
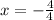
Therefore x=-1
Now substitute the value x=-1 in equation(1) we get
(-1)+3y=9
3y=9+1
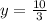
Therefore the values of x and y to the given equations are x=-1 and
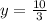
The solution is (-1,
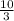 )
)