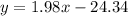Question

Use the given data to find the equation of the regression line. x 44 44 11 11 55 y 66 55 negative 1−1 negative 3−3 88 ModifyingAbove y with caretyequals=nothingplus+nothingx​ (Round to two decimal places as​ needed.)

Answer 1

`y=1.98 x -24.34`

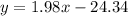
Explanation:

Assuming the following data

X: 44, 44, 11, 11, 55

Y: 66, 55, -1, -3, 88

We want to find a linear model
`Y= mx +b`

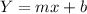
For this case we need to calculate the slope with the following formula:

`m=(S_(xy))/(S_(xx))`

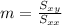
Where:

`S_(xy)=\sum_(i=1)^n x_i y_i -((\sum_(i=1)^n x_i)(\sum_(i=1)^n y_i))/(n)`

`S_(xx)=\sum_(i=1)^n x^2_i -((\sum_(i=1)^n x_i)^2)/(n)`

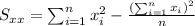
So we can find the sums like this:

`\sum_(i=1)^n x_i =44+44+11+11+55=165`

`\sum_(i=1)^n y_i =66+55-1-3+88=205`

`\sum_(i=1)^n x^2_i =7139`

`\sum_(i=1)^n y^2_i =15135`

`\sum_(i=1)^n x_i y_i =10120`

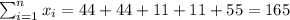
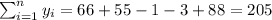
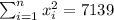
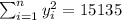
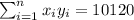
With these we can find the sums:

`S_(xx)=\sum_(i=1)^n x^2_i -((\sum_(i=1)^n x_i)^2)/(n)=7139-(165^2)/(5)=1694`

`S_(xy)=\sum_(i=1)^n x_i y_i -((\sum_(i=1)^n x_i)(\sum_(i=1)^n y_i))/(n)=10120-(165*205)/(5)=3355`

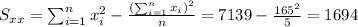
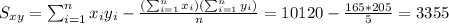
And the slope would be:

`m=(3355)/(1694)=1.98`

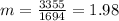
Nowe we can find the means for x and y like this:

`\bar x= (\sum x_i)/(n)=(165)/(5)=33`

`\bar y= (\sum y_i)/(n)=(205)/(5)=41`

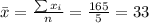
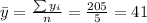
And we can find the intercept using this:

`b=\bar y -m \bar x=41-(1.98*33)=-24.34`

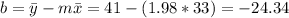
So the line would be given by:

`y=1.98 x -24.34`