Question

Aramis is adjusting a satellite because he finds it is not focusing the incoming radio waves perfectly. The shape of his satellite can be modeled by (x - 4)^2 = 3(y - 3), where x and y are modeled in inches. He realizes that the static is a result of the feed antenna shifting slightly off the focus point. Where should the feed antenna be placed?A. 0.75 in. below the vertexB. 0.75 in. to the right of the vertexC. 0.75 in. to the left of the vertexD. 0.75 in. above the vertex

Answer 1

D. 0.75 in. above the vertex

Explanation:

For this case we have the following equation for the parabola given:

`(x-4)^2 = 3 (y-3)`

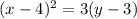
We know that the general equation for a parabola for this special case is given by:

`(x-h)^2 = 4p(y-k)`

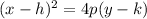
Where
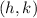`(h,k)` represent the vertex of the parabola and p the focus.

If we analyze the functional form we see that
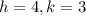`h = 4, k=3` so the vertex would be
`(4,3)`

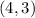
And the focus would be:

`3 = 4p`

`p =(3)/(4) =0.75`

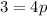
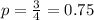
"He realizes that the static is a result of the feed antenna shifting slightly off the focus point". So then we need to move the antenna upward in order to have the vertex on the focus point and the new coordinates for the vertex are:

`(k, k+p) = (4, 3+0.75)= (4,3.75)`

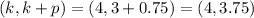
The directrix for this parabola would be:

`y = k -p = 3-0.75=2.25`

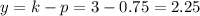
So then the parabola should be on the focus point (4,3.75) and with a directrix y =2.25.

We can see this on the figure attached.

The correct answer would be:

D. 0.75 in. above the vertex