Question

A rocket moves upward, starting from rest with an acceleration of 28.1 m/s2 for 3.01 s. It runs out of fuel at the end of the 3.01 s, but does not stop. How high does it rise above the ground?

Answer 1

491.919561014 m

Step-by-step explanation:

t = Time taken

u = Initial velocity

v = Final velocity

s = Displacement

a = Acceleration

g = Acceleration due to gravity = 9.81 m/s²

`v=u+at\\\Rightarrow v=0+28.1* 3.01\\\Rightarrow v=84.581\ m/s`

`s=ut+(1)/(2)at^2\\\Rightarrow s=0* t+(1)/(2)* 28.1* 3.01^2\\\Rightarrow s=127.294405\ m`

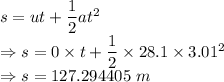
The distance at which the fuel runs out is 127.294405 m

`v^2-u^2=2gs\\\Rightarrow s=(v^2-u^2)/(2g)\\\Rightarrow s=(0^2-84.581^2)/(2* -9.81)\\\Rightarrow s=364.625156014\ m`

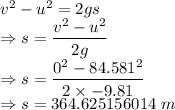
The distance covered after the engine turns off is 364.625156014 m

Total distance above the ground is 364.625156014+127.294405 = 491.919561014 m