Question

Suppose a 95% confidence interval for obtained from a random sample of size 13 is (3.5990, 19.0736). Find the lower bound of a 90% confidence interval for (round off to the nearest integer).

Answer 1

The lower bound of a 90% confidence interval = 4.83

Explanation:

Let us assume that the 95% confidence interval for population mean is constructed from a random sample of size 13 which is (3.5990, 19.0736).

We calculate 95% confidence interval for population mean by;

x bar
`\pm` 1.96
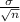`(\sigma)/(√(n) )` , where xbar = sample mean or observed mean

`\sigma` = Population standard deviation

n = sample size

1.96 = It represent that at 2.5% level of

significance the area of z score will be 1.96.

So (3.5990, 19.0736) = x bar
`\pm` 1.96
`(\sigma)/(√(13) )` , which further represent

x bar - 1.96
`(\sigma)/(√(13) )` = 3.5990 Equation 1

x bar + 1.96
`(\sigma)/(√(13) )` = 19.0736 Equation 2

Solving these two above questions we get x bar = 11.336 and
`\sigma` = 14.233

Now Similarly the 90% Confidence Interval = x bar
`\pm` 1.6449
`(\sigma)/(√(n) )`

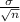
So, the lower bound for this confidence interval is = x bar - 1.6449
`(\sigma)/(√(13) )`

= 11.336 - 1.6449
`(14.233)/(√(13) )`

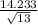
= 4.843 or 4.83

Therefore, the lower bound of a 90% confidence interval is 4.83.