Question

Natural gas at and standard atmospheric pressure of 14.7 psi (abs) is compressed isentropically to a new absolute pressure of 70 psi. Determine the final density and temperature of the gas.

Answer 1

Complete question:

Natural gas at 70 ⁰F and standard atmospheric pressure of 14.7 psi (abs) is compressed isentropically to a new absolute pressure of 70 psi. Determine the final density and temperature of the gas.

Answer:

The final density of the natural gas is 0.004243 slugs/ft³ and

The final temperature of the natural gas is 306.6 ⁰F

Step-by-step explanation:

For Ideal gas: P = ρRT

R is ideal gas constant = 3.099 x 10³ ft lb / slug⁰R

T₁ is initial temperature = 70 ⁰F = (70+460)⁰R = 530⁰R

P₁ is intial pressure of the gas = 14.7 psi = (14.7 lb/in² X 144 in²/ft²) = 2116.8 lb/ft²

From the ideal gas equation, we calculate initial density of the natural gas:

ρ₁ = P/RT ⇒ 2116.8/(3.099 x 10³ X 530) = 0.001289 slugs/ft³

For isentropic process:

`(P)/(\rho^K) = Constant`

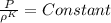
where K is the ratio of specific heats for natural gas; K = 1.31, Therefore

`(P_1)/(\rho_1^(K)) = (P_2)/(\rho_2^(K)) ,\rho_2^K = ((P_2)/(P_1))\rho_1^K , \rho_2 = ((P_2)/(P_1))^(1)/(K) \rho_1`

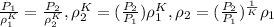
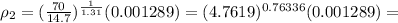`\rho_2 = ((70)/(14.7))^(1)/(1.31) (0.001289) = (4.7619)^(0.76336)(0.001289) =` 0.004243 slugs/ft³

Final density; ρ₂ = 4.243 X10⁻³ slugs/ft³

From ideal gas equation; P = ρRT

P₂ = ρ₂RT₂

T₂ = P₂/ρ₂R

P₂ (lb/ft²) = (70 lb/in²)( 144 in²/ft²) = 10080 lb/ft²

T₂ = 10080/(0.004243 X 3099)

T₂ = 766.6⁰R

Final Temperature; T₂ = (766.6-460)⁰F = 306.6⁰F