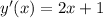Answer:
x =3.1

x =3.01
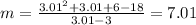
x =2.9
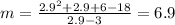
x =2.99
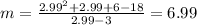
Based on the results we can conclude this condition:

And the slope would be given by:
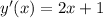
Explanation:
For this case we have defined the point P=(3,18) and Q= (x, x^2 +x+6) and we want to find the slope of the secant for the line PQ for a list of values.
The slope for the secant would be given by this formula:
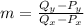
And if we replace the values for the points we got:
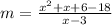
So now we just need to replace the different values for x
x =3.1

x =3.01
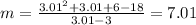
x =2.9
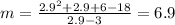
x =2.99
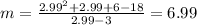
Based on the results we can conclude this condition:

And the slope would be given by: