Answer:
1. A sperm whale is 3 orders of magnitude heavier than a La Plata river dolphin; 2. The radius of the larger ball is one (1) order of magnitude bigger than the radius of the smaller ball; 3. The volume of the larger ball is 3 orders of magnitude bigger than the volume of the smaller ball.
Step-by-step explanation:
If we expressed a number as:
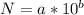 (1)
(1)
Where
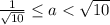 (2)
(2)
or
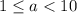 (3)
(3)
Then, b represents the order of magnitude of such a number (Order of magnitude (2020), in Wikipedia).
The order of magnitude can be defined as "...the smallest power of ten needed to represent a quantity" (Weisstein, Eric W. "Order of Magnitude". From MathWorld--A Wolfram Web Resource).
Having gathered all this information, we can proceed as follows:
First case
The La Plata river dolphin weighs between 30 and 50kg and the sperm whale weighs between 35,000 and 40,000kg.
Then, considering (1) and (3) to express the dolphin and whale's weight (since in this way the order of magnitude is the same as the exponent part in the scientific notation):
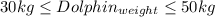
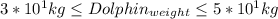

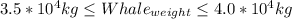
Since the range for the weights are in the same order of magnitude for both dolphin and whale (considering the definition above):
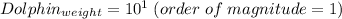
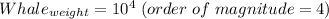
Then
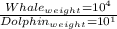
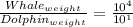

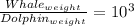
Thus
A sperm whale is 3 orders of magnitude heavier than a La Plata river dolphin.
Second case
Following the same reasoning, we can conclude that the radius of the larger ball is one (1) order of magnitude bigger than the radius of the smaller ball:
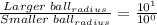
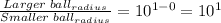
Third case
For this case, we need to calculate the volume of a sphere for both radii (1cm and 10cm).
The volume of a sphere is
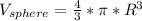
Then, the volume of the ball of radius 1cm is:
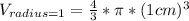
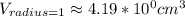
And, the volume of the ball of radius 10cm is:
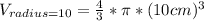
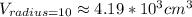
Thus
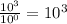
As a result, the volume of the larger ball is 3 orders of magnitude bigger than the volume of the smaller ball.