Question

A rectangular yard has a​ width-to-length ratio of 2 font size decreased by 3 : font size decreased by 3 9. If the distance around the yard is 2200 ft​, what are the dimensions of the​ yard?

Answer 1

The width of the yard will be = 200 ft

The length of the yard will be = 900 ft

Explanation:

Given:

Ratio of width to length of a rectangular yard = 2 : 9

The distance around the yard = 2200 ft

To find the dimensions of the yard.

Solution:

Let the width of the rectangular yard be =
`2x`

So, the length of the yard will be =
`9x`

The perimeter of a rectangle is given as:

`P=2(l+w)`

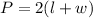
where
`l` represents length and
`w` represents width of the rectangle.

Plugging in the given values of length and width of the yard.

`P=2(9x+2x)`

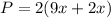
Simplifying.

`P=2(11x)`

`P=22x`

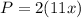
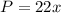
The perimeter given = 2200 ft.

Thus, the equation to find
`x` can be given as:

`22x=2200`

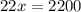
Dividing both sides by 22.

`(22x)/(22)=(2200)/(22)`

∴
`x=100`

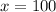
The width of the yard will be =
`2* 100 = 200\ ft`

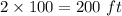
The length of the yard will be =
`9* 100 = 900\ ft`