Question

g Two force vectors are perpendicular, that is, the angle between their directions is ninety degrees. If their magnitudes are 6.65 newtons and 4.35 newtons, then what is the magnitude of their sum?

Answer 1

Resultant force will be equal to 7.946 N

Step-by-step explanation:

We have given two forces of magnitude

Magnitude of second force
`F_1=6.65N`

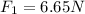
And magnitude of force
`F_2=4.35N`

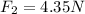
It is given that forces are perpendicular to each other

So angle between forces is
`\Theta =90^(\circ)`

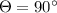
We have to find the sum of magnitude resultant force

So force
`F=√(F_1^2+F_2^2+2F_1F_2cos\Theta )`

So
`F=√(6.65^2+4.35^2+2* 6.65* 4.35* cos0 )=7.945N`

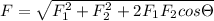
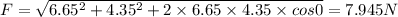
So resultant force will be equal to 7.946 N