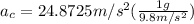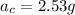Question

Our balance is maintained, at least in part, by the endolymph fluid in the inner ear. Spinning displaces this fluid, causing dizziness. Suppose a dancer (or skater) is spinning at a very fast 3.0 revolutions per second about a vertical axis through the center of the head. Although the distance varies from person to person, the inner ear is approximately 7.0 cm from the axis of spin. What is the radial acceleration (in m/s and in g's) of the endolymph fluid?

Answer 1

To solve this problem we will define the given angular velocity, in terms of international units, we will subsequently use the definition of radial acceleration, defined as the product between the square of the angular velocity and the radius. Finally we will convert the units to gravitational terms or units G.

PART A) Our values in SI are,

`\omega = 3 rev/s`

`\omega = 3 (rev)/(s) ((2\pi rad)/(1 rev))`

`\omega = 18.85rad/s`

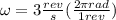
Radial acceleration can be described as

`a_c = \omega^2 R`

`a_c = (18.85)^2 (7*10^(-2))`

`a_c = 24.8726m/s^2`

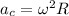
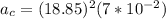
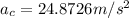
PART A) If we have that 1g is equivalent to
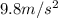`9.8m / s ^ 2` performing the conversion we have to

`a_c = 24.8725 m/s^2 ((1g)/(9.8m/s^2))`

`a_c = 2.53g`