Answer:
Volume;
Let's find the volume of the hemisphere above,
Formula for hemisphere volume:
V = 2/3πr
Where pi(π) is 22/7 or 3.14, and 'r' is the radius.
(extra info:) D/2 = radius
So, diameter in this case is 6,
6/2 = 3 is the radius.
Replace values:-
V = 2/3πr
V = 2/3 x 3.14(3)
V = 2/3 x 9.42
V = 18.84/3
V = 6.28 feet is the volume for the hemisphere.
Now the cylinder's volume,
Cylinder volume formula:
V = π
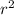 h
h
Where pi(π) is 22/7 or 3.14, 'r' is the radius which is being squared, and 'h' is the height.
Replace values (we figured out radius is 3);
V = π
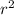 h
h
V = 3.14(3^2) x 10
V = 3.14(9) x 10
V = 28.26 x 10
V = 282.6 feet is the volume of the cylinder.
Add our volumes:-
6.28 + 282.6
= 288.88 feet is our volume.
Surface area;
Now the surface area formula of the cylinder is:
SA = 2πrh(lateral area) + 2π
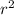 (area of circle)
(area of circle)
Replace values:
SA = 2πrh + 2π
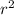
SA = 2(3.14) x 10 + 2(3.14) x 3^2
SA = 6.28 x 10 + 6.28 x 9
SA = 62.8 + 56.52
SA = 119.32 is the surface area of the cylinder.
Now the surface area formula of the hemisphere;
SA = 3πr²
Replace values;
SA = 3πr²
SA = 3(3.14) x 3^2
SA = 9.42 x 9
SA = 84.78 is the surface area of the hemisphere.
Add the areas;
119.32 + 84.78
= 204.1 feet is the surface area.