Question

Question in the below, i know it’s NOT A

Answer 1

4.
`x^{((7)/(4))} = \sqrt[7]{x^4}`

Explanation:

Here, consider the each expression and simplify it:

1.
`x^{(1)/(8) }* x^{(1)/(8)`

Now, if the BASE IS SAME when multiplied, THE POWERS ARE ADDED.

`x^{(1)/(8) }* x^{(1)/(8)} = x^{((1)/(8) + (1)/(8))}\\= x^{((1)/(4))} =\sqrt[4]{x} \\\implies x^{(1)/(8) }* x^{(1)/(8)} = \sqrt[4]{x}`

Hence, given statement if TRUE.

2.
`\frac{x^{(2)/(5) }}{x^{(1)/(5) }}`

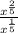
Now, if the BASE IS SAME when divided, THE POWERS ARE SUBTRACTED.

`\frac{x^{(2)/(5) }}{x^{(1)/(5) }} = x^{((2)/(5) ) -((1)/(5) )} = x^ {((1)/(5))} = \sqrt[5]{x} \\\implies \frac{x^{(2)/(5) }}{x^{(1)/(5) }} = \sqrt[5]{x}`

Hence, given statement if TRUE.

3.
`x^{((7)/(9))`

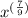
Now,a s we know :
`x^{((1)/(a)) } = \sqrt[a]{x}`

So, solving given expression:
`x^{((7)/(9))} = \sqrt[9]{x^7}`

Hence, given statement if TRUE.

4.
`x^{((7)/(4))`

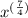
Now,a s we know :
`x^{((1)/(a)) } = \sqrt[a]{x}`

So, solving given expression:
`x^{((7)/(4))} = \sqrt[4]{x^7} \\eq \sqrt[7]{x^4}`

Hence, given statement if FALSE.

Answer 2

Option D) is correct

That is the rational exponent expression is not simplified correctly is

`x^{(7)/(4)=\sqrt[7]{x^4}`

Explanation:

Given rational exponent expression is
`x^{(7)/(4)=\sqrt[7]{x^4}`

To prove that LHS=RHS

First taking LHS

`x^{(7)/(4)`

`=(x^7)^{(1)/(4)}`

`=\sqrt[4]{x^7}`

Therefore
`x^{(7)/(4)=\sqrt[4]{x^7}\\eq RHS`

But we have
`x^{(7)/(4)=\sqrt[7]{x^4}`

Therefore
`LHS\\eq RHS`

The corrected simplified expression
`x^{(7)/(4)=\sqrt[4]{x^7}`

Therefore Option D) is correct

Therefore the rational exponent expression which is not simplified correctly is

`x^{(7)/(4)=\sqrt[7]{x^4}`