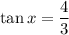Question

A right angle triangle is shown with hypotenuse equal to 10 centimeters. An acute angle of the triangle is labeled as x degrees

What is the value of tan x°?

Answer 1

The Question is incomplete the Complete Question is

Look at the triangle: A right angle triangle is shown with hypotenuse equal to 10 centimeters. An acute angle of the triangle is labeled as x degrees. The side adjacent to the acute angle has length 6 centimeters and the side opposite to the acute angle has length 8 centimeters. What is the value of tan x°?

Answer:

Therefore the value of tan x is

`\tan x=(4)/(3)`

Explanation:

Given:

hypotenuse = 10 cm'

side adjacent to the acute angle 'x' = 6 cm.

side opposite to the acute angle 'x' = 8 cm.

To Find:

tan x = ?

Solution:

In Right Angle Triangle , Tan Identity we have

`\tan x= \frac{\textrm{side opposite to angle x}}{\textrm{side adjacent to angle x}}`

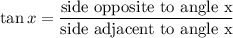
Substituting the values we get

`\tan x= (8)/(6)=(4)/(3)`

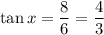
Therefore the value of tan x is

`\tan x=(4)/(3)`