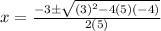Question

Which equation shows the quadratic formula used correctly to solve 5x2 + 3x - 4 = 0 for x?

- 3+ √(3) ² - 4 (6) (-4)
2(5)
3+ (3) +45)(-4)
X
3+ (3)2-4(5)(-4)
OX=
- 3+ √(3)² + 4 (5)(-4)
205)

Answer 1

A) −3

Step-by-step explanation:

Answer 2

The quadratic formula used to solve the equation
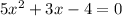`5x^(2) +3x-4=0` is
`x=\frac{-3 \pm \sqrt{(3)^(2)-4(5)(-4)}}{2(5)}`

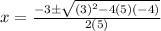
Step-by-step explanation:

The equation is
`5x^(2) +3x-4=0`

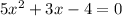
The equation is of the form
`ax^(2) +bx+c=0`

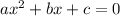
Thus,
`a=5, b=3,c=-4`

To find the quadratic formula, the general formula to find the quadratic roots is
`x=\frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}`

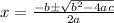
Hence, substituting the values of a,b,c in the formula, we get,

`x=\frac{-3 \pm \sqrt{(3)^(2)-4(5)(-4)}}{2(5)}`

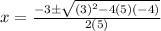
Thus, Option A is the correct answer.

The quadratic formula used to solve the equation
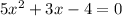`5x^(2) +3x-4=0` is
`x=\frac{-3 \pm \sqrt{(3)^(2)-4(5)(-4)}}{2(5)}`