Answer:
The value to the given expression is 8
Therefore
![\left[((10^4)(5^2))/((10^3)(5^3))\right]^3=8](https://img.qammunity.org/2021/formulas/mathematics/middle-school/rek18l5dg34bfe0yzrled5t9vmybloaevw.png)
Explanation:
Given expression is (StartFraction (10 Superscript 4 Baseline) (5 squared) Over (10 cubed) (5 cubed)) cubed
Given expression can be written as below
![\left[((10^4)(5^2))/((10^3)(5^3))\right]^3](https://img.qammunity.org/2021/formulas/mathematics/middle-school/d1vpf7x402cd5x06lniidkruao1pzon4ar.png)
To find the value of the given expression:
![\left[((10^4)(5^2))/((10^3)(5^3))\right]^3=(((10^4)(5^2))^3)/(((10^3)(5^3))^3)](https://img.qammunity.org/2021/formulas/mathematics/middle-school/de7hqfkab3o8fglv4o73qjd0ku1ux7031a.png)
( By using the property (
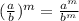 )
)
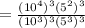
( By using the property
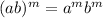 )
)
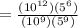
( By using the property
 )
)
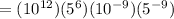
( By using the property
 )
)
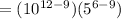 (By using the property
(By using the property
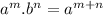 )
)

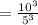 ( By using the property
( By using the property
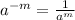 )
)
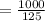
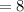
Therefore
![\left[((10^4)(5^2))/((10^3)(5^3))\right]^3=8](https://img.qammunity.org/2021/formulas/mathematics/middle-school/rek18l5dg34bfe0yzrled5t9vmybloaevw.png)
Therefore the value to the given expression is 8