Question

Given the functions f(x)=1x−3+1 and g(x)=1x+4+3 .

Which statement describes the transformation of the graph of function f onto the graph of function g?




The graph shifts 7 units left and 2 units up.

The graph shifts 7 units right and 2 units down.

The graph shifts 2 units right and 7 units down.

The graph shifts 2 units left and 7 units up.

Answer 1

A. The graph shifts 7 units left and 2 units up.

Explanation:

Be careful to make sure you got the right answer and not just "A"
The order tends to change
Best of luck to you~!

Answer 2

The graph shifts 7 units left and 2 units up.

Explanation:

In transformations, when a number is added or subtracted to "x" directly, that is the left/right shift.

When a number is added or subtracted outside of the "rest" of the equation, that is the up/down shift.

I learned transformations with these variables:

`f(x) = (a)/(k(x-c)) + d`

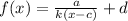
"a" - vertical stretch (a > 1) or compression (0 < a < 1)

"k" - horizontal stretch (0 < k < 1) or compression (k > 1)

"c" - translate left (+) or right (-)

"d" - translation up (+) or down (-)

The untranslated graph is centred around the origin f(x) = 1/x

f(x) begins 3 units right and 1 unit up of the untranslated graph.

g(x) is 4 units left and 3 units up of the untranslated graph.

y

g |

| f

-----------|------------ x

There is a 7 units translation left and 2 units translation up.