Question

What is the minimum point on a graph of f(x) = (x - 1)² - 3?

(1, -3)
(-1, -3)
(-3, 1)
(-2, -2)

Answer 1

(1, -3)

First option

Explanation:

The minimum point on the graph is also the vertex.

The quadratic function equation is given in vertex form, which is
`f(x) = a(x - h)^(2) + k`

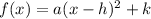
Using this equation, the vertex is (-h, k).

Whatever number you see for "h", find its opposite negative/positive. That will be the x-coordinate of the vertex. The y-coordinate for the vertex is the same as "k", keeping the negative and positive.

In f(x) = (x - 1)² - 3 using (-h, k) is:

h = -1 => -h = 1

k = -3

Therefore the vertex is (1, -3).