Answer:
The value of
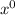 is
is
 .
.
Explanation:
The figure provided to is a rectangle, named ABDC.
All the angles, m∠CAB = m∠ABD= m∠BDC = m∠DCA =
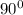 .
.
The lines AD and BC are diagonals of the rectangle ABDC.
According to the diagonal property of rectangles, they bisect each other.
Then,
- m∠CED = m∠AEB and m∠BED = m∠AEC
- AE = BE, CE = ED
- The opposite angle at the points where the diagonals meet are congruent, i.e. m∠DAB = m∠ADC and m∠DCB = m∠ABC.
Now, consider the triangle CED.
Since the triangle CED has two equal sides, i.e. CE = ED, it is an isosceles triangle. And hence the angles m∠DCE = m∠EDC =
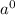 (say).
(say).
Compute the value of m∠DCE and m∠EDC using the sum of angles property of a triangle i.e. the sum of all three angles of a triangle is
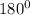 .
.
Solve for
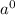 as follows:
as follows:
m∠CED + m∠ECD + m∠EDC =
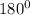
 +
+
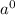 +
+
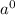 =
=
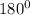
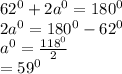
So, m∠EDC =
 = m∠ADC.
= m∠ADC.
As the opposite angles at the points where the diagonals meet are congruent, then,
m∠DAB = m∠ADC =
 .
.
Thus, the value of
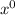 is
is
 .
.