Answer:
(3, 1)
Explanation:
To find the solution (point of intersection) of a system of linear equations, first convert them to slope-intercept form (y=mx+b) by isolating "y". Then, equate their expressions to find "x". Substitute what you find for "x" to find the coordinate for "y".
Isolate "y" in each equation
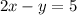 Subtract 2x from both sides
Subtract 2x from both sides
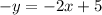 Divide the whole equation by -1 to isolate "y"
Divide the whole equation by -1 to isolate "y"
 Each term's negative/positive sign changes
Each term's negative/positive sign changes
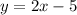
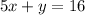 Subtract 5x from both sides
Subtract 5x from both sides
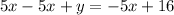 The 5x on left cancel out (5x - 5x = 0)
The 5x on left cancel out (5x - 5x = 0)

Since y = 2x - 5 and y = -5x + 16 both equal y, we can make them equal each other. Then isolate "x" to be on the left side.
Equate the equations
y = y
2x - 5 = -5x + 16
2x - 5 + 5x = -5x + 5x + 16 Add 5x to both sides
2x - 5 + 5x = 16 Right side 5x cancelled out (-5x + 5x = 0)
7x - 5 = 16 Combined like terms on left (2x + 5x = 7x)
7x - 5 + 5 = 16 + 5 Add 5 to both sides.
7x = 16 + 5 Left side cancelled out (-5 + 5 = 0)
7x = 21 Simplified right side.
7x/7 = 21/7 Divide both sides by 7
x = 21/7 Since 7/7=1, 7x/7 = x , and "x" is isolated.
x = 3 Found "x" coordinate of solution.
Substitute x = 3 into any equation
2x - y = 5
2(3) - y = 5 Simplify first by multiplying 2 and 3 on left side
6 - y = 5 Start isolating "x"
6 - y + y = 5 + y Add "y" to both sides.
6 = 5 + y Left side y's cancelled out (-y + y = 0)
6 - 5 = 5 - 5 + y Subtract 5 from both sides
6 - 5 = y Right side cancelled out (5 - 5 = 0)
1 = y Answer after left side simplified (6 - 5=1)
y = 1 Standard formatting puts variable on left
Write the solution as an ordered pair in the form (x, y).
The solution to the linear system is (3, 1).
Check if this is correct by substituting x=3 and y=1 into both equations:
2x - y = 5
2(3) - 1 = 5 Simplify 2 times 3
6 - 1 = 5 Subtract
5 = 5 Same answer
LS = RS Left side equals right side
Correct
5x + y = 16
5(3) + 1 = 16 Simplify 5 times 3
15 + 1 = 16 Add
16 = 16 Same answer
LS = RS Left side equals right side
Correct.