Question

f(x) is a quadratic function with x-intercepts at (−1, 0) and (−3, 0). If the range of f(x) is [−4, [infinity]) and g(x) = 2x^2 + 8x + 6, compare f(x) and g(x). Select the statement that is not correct?

Answer 1

Answer with Step-by-step explanation:

We are given that function f(x) which is quadratic function.

x -intercept of function f(x) at (-1,0) and (-3,0)

x-Intercept of f means zeroes of f

x=-1 and x=-3

Range of f =[-4,
`\infty`)

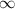g(x)=
`2x^2+8x+6=2(x^2+4x+3)`

`g(x)=0`

`2(x^2+4x+3)=0`

`x^2+4x+3=0`

`x^2+3x+x+3=0`

`x(x+3)+1(x+3)=0`

`(x+1)(x+3)=0`

`x+1=0\implies x=-1`

`x+3=0\implies x=-3`

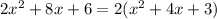
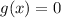
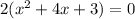
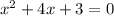
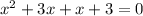
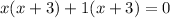
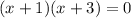
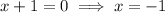
Therefore, x-intercept of g(x) at (-1,0) and (-3,0).

Substitute x=-2

`g(-2)=2(-2)^2+8(-2)+6=8-16+6=-2`

`g(x)=2(x^2+4x)+6`

`g(x)=2(x^2+2* x* 2+4-4)+6=2(x^2+2* x* 2+4)-8+6`

`g(x)=2(x+2)^2-2`

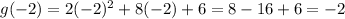
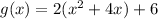
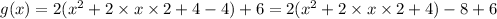
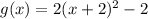
By comparing with the equation of parabola

`y=a(x-h)^2+k`

Where vertex=(h,k)

We get vertex of g(x)=(-2,-2)

Range of g(x)=[-2,
`\infty`)

Zeroes of f and g are same .

But range of f and g are different.

Range of f contains -3 and -4 but range of g does not contain -3 and -4.

f and g are both quadratic functions.