Answer:
The solved expression is
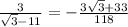
Explanation:
Given expression is
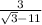
To rationalize the given expression as below :
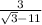
Multiply and divide the conjugate of denominator
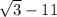 is
is
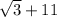 we get
we get
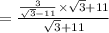
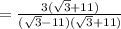
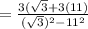 ( using the formula
( using the formula
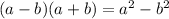 )
)
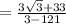
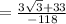
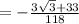
Therefore the solved expression is
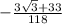
Therefore the given expression is
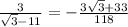 .
.