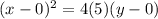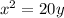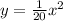Question

The equation of the parabola whose focus is at (0, 5) and directrix at y = -5 is:

y = (1/20)x²
x = (1/20)y²
y = -(1/20)x²

Answer 1

`y=(1)/(20)x^2`

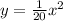
Explanation:

In this problem

we have

F(0,5) and directrix at y=-5

so

Is a vertical parabola open upward

we know that

The equation of a vertical parabola in standard form is

`(x-h)^2=4p(y-k)`

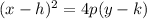
where

p is the focal distance

(h,k) is the vertex

we have

The vertex is the origin (0,0)

and

p=5

substitute

`(x-0)^2=4(5)(y-0)`

`x^2=20y`

`y=(1)/(20)x^2`