Answer:
a) Null hypothesis:
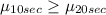
Alternative hypothesis:
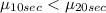
The statistic calculated was t= -5.57 with a p value of p=0.000001353, a very low value so we have enough evidence to reject the null hypothesis on this case. So then we can conclude that more time cooling result in a lower number of defects
b)

c)
 . And as we can see all the values are <0. We conclude that the two samples are different on the mean. And the group of 20 seconds seems better result.
. And as we can see all the values are <0. We conclude that the two samples are different on the mean. And the group of 20 seconds seems better result.
d) We can see this on the figure attached. And we see that the values for the group of 20 seconds are significantly higher than the values for the group of 10 seconds.
e) The results are on the figure attached. And as we can see the results are not significant different from the normal distribution since almost all the values for both graphs lies in the line adjusted.
Explanation:
Assuming the following data:
Sample 1 (10 seconds) : 1,3,2,6,1,5,3,3,5,2,1,1,5,6,2,8,3,2,5,3
Sample 2(20 seconds): 7,6,8,9,5,5,9,7,5,4,8,6,6,8,4,5,6,8,7,7
Part a: Is there evidence to support the claim that the longer cool-down time results in fewer appearance defects? Use α = 0.05.
Null hypothesis:
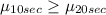
Alternative hypothesis:
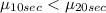
For this case we can use the following R code:
> sample1<-c(1,3,2,6,1,5,3,3,5,2,1,1,5,6,2,8,3,2,5,3)
> sample2<-c(7,6,8,9,5,5,9,7,5,4,8,6,6,8,4,5,6,8,7,7)
> t.test(sample1,sample2,conf.level = 0.95,alternative = "less")
The results obtained are:
Welch Two Sample t-test
data: sample1 and sample2
t = -5.5696, df = 35.601, p-value = 1.353e-06
alternative hypothesis: true difference in means is less than 0
95 percent confidence interval:
-Inf -2.194869
sample estimates:
mean of x mean of y
3.35 6.50
And as we can see the statistic calculated was t= -5.57 with a p value of p=0.000001353, a very low value so we have enough evidence to reject the null hypothesis on this case. So then we can conclude that more time cooling result in a lower number of defects
Part b: What is the P-value for the test conducted in part (a)?

Part c: Find a 95% confidence interval on the difference in means. Provide a practical interpretation of this interval.
From the output given we see that the confidence interval obtained was:
 . And as we can see all the values are <0. We conclude that the two samples are different on the mean. And the group of 20 seconds seems better result.
. And as we can see all the values are <0. We conclude that the two samples are different on the mean. And the group of 20 seconds seems better result.
Part d: Draw dot diagrams to assist in interpreting the results from this experiment
We can see this on the figure attached. And we see that the values for the group of 20 seconds are significantly higher than the values for the group of 10 seconds.
Part e :Check the assumption of normality for the data from this experiment.
We can use the following R code:
> qqnorm(sample1, pch = 1, frame = FALSE,main = "10 seconds")
> qqline(sample1, col = "steelblue", lwd = 2)
> qqnorm(sample2, pch = 1, frame = FALSE,main = "20 seconds")
> qqline(sample2, col = "steelblue", lwd = 2)
The results are on the figure attached. And as we can see the results are not significant different from the normal distribution since almost all the values for both graphs lies in the line adjusted.