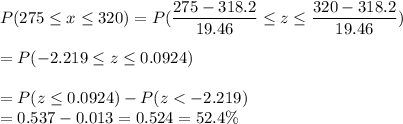Question

The taxi and takeoff time for commercial jets is a random variable x with a mean of 8.6 minutes and a standard deviation of 3.2 minutes. Assume that the distribution of taxi and takeoff times is approximately normal. You may assume that the jets are lined up on a runway so that one taxies and takes off immediately after the other, and that they take off one at a time on a given runway. (a) What is the probability that for 37 jets on a given runway, total taxi and takeoff time will be less than 320 minutes?(b) What is the probability that for 37 jets on a given runway, total taxi and takeoff time will be more than 275 minutes?

(c) What is the probability that for 37 jets on a given runway, total taxi and takeoff time will be between 275 and 320 minutes?

Answer 1

a) 0.537

b) 0.987

c) 0.524

Explanation:

We are given the following information in the question:

We are given that the distribution of the taxis and takeoff times is a bell shaped distribution that is a normal distribution.

Formula:

`z_(score) = \displaystyle(x-\mu)/(\sigma)`

Sample size, n = 37

The central limit theorem says that the sum of n measurement is approximately normal to
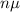`n\mu` and
`\sigma √(n)`

`\mu = 37* 8.6 = 318.2\\\sigma√(n) = 3.2* √(37) = 19.46`

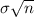
a) P(takeoff time will be less than 320 minutes)

P(x < 320)

`P( x < 320) = P( z < \displaystyle(320 - 318.2)/(19.46)) = P(z < 0.0924)`

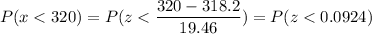
Calculation the value from standard normal z table, we have,

`P(x< 320) = 0.537 = 53.7\%`

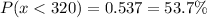
b) P( takeoff time will be more than 275 minutes)

P(x > 275)

`P( x > 275) = P( z > \displaystyle(275 - 318.2)/(19.46)) = P(z > -2.219)`

`= 1 - P(z \leq -2.219)`

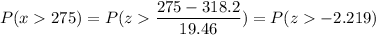
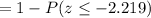
Calculation the value from standard normal z table, we have,

`P(x > 275) = 1 - 0.013 = 0.987= 98.7\%`

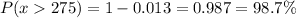
c) P( takeoff time will be between 275 and 320 minutes)

`P(275 \leq x \leq 320) = P(\displaystyle(275 - 318.2)/(19.46) \leq z \leq \displaystyle(320 - 318.2)/(19.46))\\\\=P(-2.219 \leq z \leq 0.0924)\\\\= P(z \leq 0.0924) - P(z < -2.219)\\= 0.537 - 0.013 = 0.524 = 52.4\%`

`P(275 \leq x \leq 320) = 52.4\%`