Question

The pressure gauge shown below has a spring for which k = 60 N/m, and the area of the piston is 0.50 cm2. Its right end is connected to a closed container of gas at a gauge pressure of 30 kPa. How far will the spring be compressed if the region containing the spring is (a) in vacuum, and (b) open to the atmosphere? Atmospheric pressure is 101 kPa; use Hooke’s law

Answer 1

0.025 m

0.059166 m

Step-by-step explanation:

P = Pressure

A = Area

x = Compression of spring

Force is given by

`F=PA\\\Rightarrow F=30000* 0.5* 10^(-4)\\\Rightarrow F=1.5\ N`

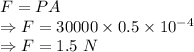
From Hooke's law

`F=kx\\\Rightarrow x=(F)/(k)\\\Rightarrow x=(1.5)/(60)\\\Rightarrow x=0.025\ m`

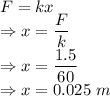
The spring is compressed 0.025 m

In the second case

`F_1=1.5\ N`

`F_2=101000* 0.5* 10^(-4)\\\Rightarrow F_2=5.05\ N`

Net force would be

`F=F_2-F_1\\\Rightarrow F=5.05-1.5\\\Rightarrow F=3.55\ N`

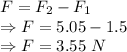
Compression would be

`x=(F)/(k)\\\Rightarrow x=(3.55)/(60)\\\Rightarrow x=0.059167\ m`

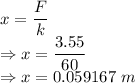
The compression of the spring is 0.059166 m